Introduction to Game Rotation
You can also see this article in my medium post.
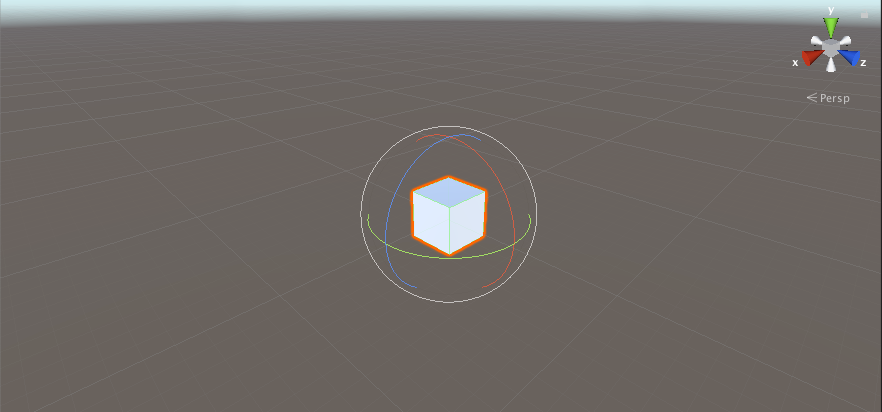
我在接觸3D遊戲引擎時,一開始對旋轉這件事感到很困擾,
在Unity的編輯器中,旋轉的表現形式看起來像三個顏色的球狀旋轉。在Transform裡面又是有著3個數字的向量形式,到了程式碼裡面,又變成Quaternion這種資料形式,讓人一時之間很難搞懂。
這篇文章會記錄一些我對於旋轉的表示方法、各種表示方法的優缺點的理解,以及使用上的一些轉換方式。最後再用一個範例,在Unity中藉由滑鼠拖拉旋轉攝影機來表示如何用程式簡單控制旋轉。
三維空間中的旋轉表示
最為常見的用法有三種:矩陣、歐拉角以及四元數
矩陣(Rotation Matrix)
矩陣方式就是我們所熟知的旋轉矩陣,利用一個3×3矩陣,表示從一個基準的座標,旋轉到目標的座標所使用的旋轉矩陣,換言之,矩陣形式就是將旋轉表示(orientation)轉換成旋轉表示的數學形式。
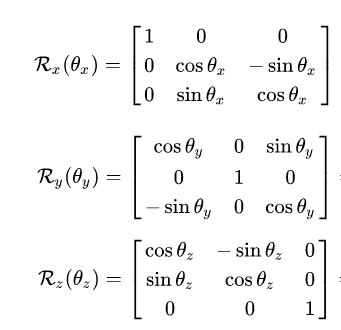
利用矩陣形式的最大優點,就是對於三維空間座標的向量旋轉是可以立刻使用的,並且可以簡單取得相對的角位移(angular displacement)。
而缺點部分就是相對於其他旋轉的表示方法,需要花到9個數字的儲存空間,並且經常會造成浪費,因為時常我們可能只需要相對某個轉軸的旋轉。
歐拉角(Euler Angle)
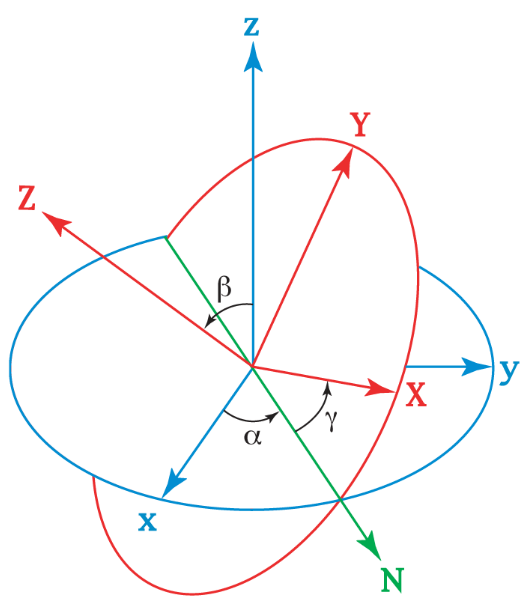
歐拉角是將旋轉的定義,從用數字一次定義出來,改變為依照順序對不同軸向進行旋轉,依照heading-pitch-bank定義三個旋轉為heading angle, pitch angle以及bank angle。Heading rotation是沿著y軸進行旋轉,Pitch rotation沿著x軸進行旋轉,Bank rotation則是沿著z軸進行旋轉,字面上定義依照這個順序進行歐拉角的旋轉。
值得注意的是,歐拉角的旋轉不只有heading-pitch-bank方式,還有roll-pitch-yaw等不同的旋轉方式以及順序,像在Unity中,就是以這種方式旋轉,Unity的歐拉角的旋轉順序是沿著Z軸旋轉(roll),再來沿著X軸旋轉(pitch),最後沿著Y軸旋轉(yaw)。
歐拉角的最大的優點,就是歐拉角對於閱讀起來十分直觀,是人類可以直接判別的旋轉方法。此外,歐拉角也是對於旋轉最為簡潔的表達方法,只需要3個數字就可以表達出一個旋轉,是最為節省記憶體的方法。
但是,看似如此方便的歐拉角,卻存在著兩個非常嚴重的缺點:
1. 表示同樣旋轉的歐拉角並不唯一
也被稱作別名(aliasing)問題,例如在角度上加上360度,就是一種最單純的別名問題,因為對角度加上360度並不會改變他的角度。但是這類別名問題只要限制角度範圍就可以解決,並不會造成太大的困擾。
真正麻煩的是第二種,因為三個角度並不互相獨立的造成的問題,例如pitch 135度與 heading 180度加上pitch 45度(向下旋轉)是等價的旋轉表示。對於這種別名問題,常見的做法是限制他的旋轉角度,例如限制heading/bank在 -180 ~ +180之間,將pitch限制在-90 ~ +90之間。
然而,就算限制了上面所說的角度之後,仍然會存在一個問題,被稱為萬向鎖(Gimbal Lock),最為著名的舉例就是先head 45度再pitch 90度,與先pitch 90度再banking 45度是相同的,其最根本的原因就是pitch ±90度之後,使得另外兩個轉軸重疊,此時兩個轉軸旋轉任意角度都會造成別名問題。

為了消除萬向鎖造成的別名問題,可以規定萬向鎖發生時,只交由某一個軸去完成旋轉,假如約定以heading完成全部旋轉,bank在萬向鎖發生時就會永遠為0。
2. 對於兩個旋轉表示的內插(Lerp)的問題
角度的內差第一個會面對的問題,是歐拉角旋轉的週期性所產生的,例如要從heading -150旋轉到heading 150,就存在著60度的短弧與300度的長弧之分,解決這類問題就是將插值的差角限制到正負180度內,確保旋轉在最短弧上。
而在旋轉角度內插上,歐拉角會遇到最大的問題,還是前面提的萬向鎖問題。在單純地將歐拉角進行差值運算時,如果遇到萬向鎖問題,大多情況會導致錯誤的路徑,抖動等等問題,在萬向鎖情況旋轉歐拉角,需要將兩個角度分開旋轉,但是以攝影機的轉向操作為例,在球面上光滑旋轉才是最舒適的表現方式。而歐拉角在旋轉上所遇到的萬向鎖問題,很不幸的目前並沒有任何好的數學解法,這也是歐拉角沒辦法作為最主要旋轉表示的主要原因。
More information : https://www.youtube.com/watch?v=zc8b2Jo7mno
四元數(Quaternion)
四元數的定義
四元數原先是一個四維的複數空間的表示方法,在幾何上的應用,可以作為一種旋轉的表示方式。數值上,存在一個定標器(scaler)w以及一組三維向量v或是直接拆分成x,y,z(Unity中,可以直接取得w,x,y,z四個數值)。
四元數可以代表一個複數空間中的座標,其中[w, (x, y ,z)]被定義成w+xi+yj+zk。其中的i,j,k有如同二維複數空間的性質:
如同二維空間的複數座標可以旋轉二維向量,四元數也可以拿來旋轉三維向量。
而四元數中的四個數字究竟是什麼意思呢?從歐拉角我們可以得知,一個三維的旋轉表示可以被表述成一個旋轉軸加上一個旋轉角度,四元數也是用這個概念表示的,假設有一個旋轉軸n加上旋轉角度θ,整個四元數可以被表示成:
四元數的性質們
完全沒有旋轉的四元數被稱為identity,數值為[1,0]和[-1,0],其中的0表示零向量。
在旋轉表示的用途中,我們只使用單位四元數(Unit Quaternion),即模數為1的四元數。
- 四元數的運算
- 四元數的乘法沒有交換律,q1q2 ≠ q2q1。
- 四元數的乘法存在結合律, (q1q2)q3 = q1(q2q3)
- 四元數的乘積的模數等於模數的乘積(||q1|| ||q2|| = ||q1q2||)
- 四元數的乘法可以表示兩個旋轉的結合,進行q1再進行q2,可以合併成q3 = q2q1(旋轉順序由右向左)
- 四元數的旋轉差為反四元數,q1到q2的旋轉量為:d = (q1^-1) q2
還有許多未提到的四元數運算如點積、Quaternion Interpolation(Slerp)等,在基礎篇裡面就先省略,如果有下一篇再補上相關資訊<( )>。
四元數的優點是可以平滑插值計算,並且可以快速計算角位移以及轉換成旋轉矩陣,而且只用到四個數字進行存取,記憶體消耗較低。
四元數的缺點則是跟矩陣類似,相較歐拉角更大的記憶體用量,並且比旋轉矩陣更難直接讓人類判讀。
轉換成四元數
在Unity引擎裡面,Transform所顯示的旋轉角度是歐拉角,腳本上取得的Rotation則是四元數,理解兩者之間的轉換方式可以讓使用上更為方便。
為了更符合Unity內的使用,在這個段落中,歐拉角的表示方式將使用roll-pitch-yaw來表示。
將歐拉角轉換成四元數
在前面我們了解到,四元數可以藉由相乘來完成連續旋轉,所以我們將把rolling, pitching, yawing分為三個四元數進行旋轉,最後再將它們串成同一個四元數。
根據四元數的定義,可以轉換如下:
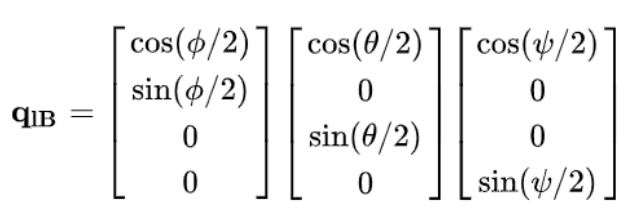
Reference
Wikipedia:
https://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles
https://en.wikipedia.org/wiki/Quaternion
3D Math Primer For Graphics and Game Development:
Amazon : https://www.amazon.com/Math-Primer-Graphics-Game-Development-ebook/dp/B008KZU548
Unity Rotation Guide:
https://docs.unity3d.com/Manual/QuaternionAndEulerRotationsInUnity.html